Differentiation

ln(e) = 1

Power Rule

Example: What is x³ ?

The question is asking "what is the derivative of x³?"

We can use the Power Rule, where n=3:

xⁿ = nxⁿ⁻¹

x³ = 3x³⁻¹ = 3x²

Example: What is (1/x) ?

1/x is also x^-1

We can use the Power Rule, where n = −1:

xⁿ = nxⁿ⁻¹

x⁻¹ = −1x⁻¹⁻¹ = −x⁻²

Multiplication by constant

Example: What is 5x³ ?

the derivative of cf = cf’

the derivative of 5f = 5f’

We know (from the Power Rule):

x³ = 3x³⁻¹ = 3x²

So:

5x³ = 5x³ = 5 × 3x² = 15x²

Sum Rule

Example: What is the derivative of x²+x³ ?

The Sum Rule says:

the derivative of f + g = f’ + g’

So we can work out each derivative separately and then add them.

Using the Power Rule:

• x² = 2x
• x³ = 3x²

And so:

the derivative of x² + x³ = 2x + 3x²

Difference Rule

It doesn't have to be x, we can differentiate with respect to, for example, v:

Example: What is 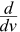(v³−v⁴) ?

The Difference Rule says

the derivative of f − g = f’ − g’

So we can work out each derivative separately and then subtract them.

Using the Power Rule:

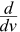• v³ = 3v²
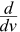• v⁴ = 4v³

And so:

the derivative of v³ − v⁴ = 3v² − 4v³

Sum, Difference, Constant Multiplication And Power Rules

Example: What is 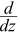(5z² + z³ − 7z⁴) ?

Using the Power Rule:

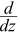• z² = 2z
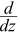• z³ = 3z²
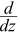• z⁴ = 4z³

And so:

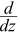
(5z² + z³ − 7z⁴) = 5 × 2z + 3z² − 7 × 4z³ = 10z + 3z² − 28z³

Example: What is the derivative of cos(x)sin(x) ?

The Product Rule says:

the derivative of fg = f g’ + f’ g

In our case:

• f = cos
• g = sin

We know (from the table above):

• cos(x) = −sin(x)
• sin(x) = cos(x)

So:

the derivative of cos(x)sin(x) = cos(x)cos(x) − sin(x)sin(x)